Fractals—A Bridge to the Future for Soil Science
Soil scientists have at least one thing in common with stockbrokers: Both deal with subjects so complex they often seem unmanageable. It should be no surprise that both are turning to a mathematics of chaos—for solutions.
The mathematician Benoit Mandelbrot is largely responsible for the current interest in fractal geometry, a math that shows the irregular shapes of nature. He first attempted to use it to master the commodities market in the 1950s. In the early 1960s, he went on to work for IBM, where he developed the computer power that fuels today's fractal frenzy.
Fractal geometry is particularly suited to advanced computer graphics packages. It has gained widespread attention of soil scientists and agronomists over the past decade. For fractal geometry may open a gate in a wall many of them run into as they gather data on several different scales.
It used to be that soil scientists interested in soil hydrology gathered data only on a small scale—either 2- by 2-inch soil samples for lab studies or 6- by 6-foot plots in the field, says Yakov Pachepsky. He is an Agricultural Research Service cooperating soil scientist from Duke University in Durham, North Carolina. [For more things that fractal mathematics can be used for, see "A Geometric Language for the Universe."
"But approach that was 20 years ago," says Pachepsky, who is currently located at the ARS Remote Sensing and Modeling Laboratory in Beltsville, Maryland.
"Now, with precision agriculture, we are asked to deal with combine-mounted yield monitors that churn out data on about 20-square-yard grids as fast as the farmer's combine crosses the field," he says. "And satellites send images of Earth on grids of a square mile or more.
"We'll be out of business if we can't relate data between all these scales. Fractal geometry offers the potential of bridging them."
Fractal geometry gets its name from the irregular fragments it deals with. It is scale-independent, which means that a basic shape stays the same—along with any objective measurements of it—no matter how much you enlarge or reduce the size of its image.
Traditional measurements are made in dimensions of line, area, volume, or mass. Fractal dimensions range from 1 for a straight line to almost 2 for a chaotic, unpredictable squiggle—like a day of extreme highs and lows on the stock market.
Fractal Dimensions Can Indicate Plant Stress
In an ARS-funded study, soil scientist Bahman Eghball at the University of Nebraska at Lincoln used fractal geometry to identify corn roots stressed by lack of nitrogen fertilizer. He dyed and photographed the roots. Then he projected the photographic slides on three different-sized grids.
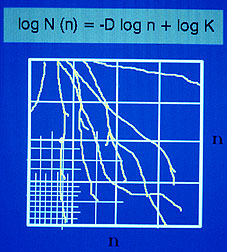
"If one or more roots fell into a grid, we counted the grid as one intersected by roots," Eghball says. By plotting the logarithm of the number of grids the roots intersected against the logarithm of grid sizes, Eghball obtained a line. The slope of that line is the fractal dimension.
Eghball found this dimension could be used to spot plant stress. When corn plants were grown without nitrogen fertilizer, roots stopped branching out, intersecting fewer grids. The result was a lower fractal dimension. That dimension, once fed into a computer graphics program with a fractal package, could be used to generate a computer image of the roots.
Eghball has used the perspective of fractal geometry to see some surprising things in the world of agriculture. For example, by analyzing 60 years of USDA crop yield statistics—1930 to 1990—he found that oats and soybeans were the riskiest crops in terms of having the most year-to-year yield fluctuations in response to weather. He also found that the Green Revolution of the 1950s and 1960s not only raised yields, but also raised risks of year-to-year yield variation.
Eghball explains that the comparison of 10 different crops with wide variations in yields was possible only with a tool like fractal geometry.
"The fractal dimension is unaffected by the fact that oat yields are much lower than corn or soybean yields," he says. "For that matter, it can compare 'apples and oranges'—or a fiber crop like cotton with a grain crop like corn. This is possible because we are comparing patterns of behavior of objects, not the objects themselves."
Eghball says another strength of fractal geometry is its ability to determine if a phenomenon is predictable. Generally, a fractal dimension close to 1 means it is more predictable. So rice yield (1.2) is more predictable than oat (1.47) or soybean (1.45) yields.
Fractals and the Chaos of Spatial Variability
One of the chaotic messes in the agronomy world is what scientists call spatial variability. That is, whatever you talk about in a farm field—crop yield, erosion, soil moisture, soil temperature, drainage, waterflow, chemical movement, soil fertility—all can vary widely, even in a space as small as 10 feet. So how can we extrapolate to thousands of acres of land without costly measurements every few feet or so? Laj Ahuja wants to see if fractal analysis can help. He uses it to quantify spatial variability so it can be plugged into computer models at his Fort Collins, Colorado, research unit. The models do not currently account for this variability.
"Precision farming has an interest in quantifying and mapping this spatial variability on landscapes so farmers can manage different parts differently," says Ahuja, who heads ARS' Great Plains System Research Unit in Fort Collins.
With the help of ARS colleagues and scientists at Colorado State University, Ahuja is trying to bridge plot, field, and farm scales so he can predict these processes across entire watersheds encompassing many farms and ranches.
Pachepsky and microbiologist Lawrence J. Sikora at Beltsville, working with soil scientist Martin Rabenhorst at the nearby University of Maryland at College Park, want to use fractal dimensions of physical aspects of soil—such as the volume and inner surface roughness of soil pores—to characterize soil quality relative to its ability to grow plants.
"These are easy-to-measure characteristics," Pachepsky says. The scientists make their measurements from thinly sliced sheets of soil samples, the structure of which is preserved by the addition of resin.
Walter J. Rawls, who heads Beltsville's ARS Hydrology Laboratory, is working with soil scientist Raymond R. Allmaras at St. Paul, Minnesota, and others to predict soil water movement based on these pore measurements, along with measurements of the soil's density and ability to hold water. They use fractal geometry to relate difficult-to-measure soil hydraulic properties to other soil variables readily available from soil surveys.
|
|
Soil scientist Jerry C. Ritchie, who is also with the Hydrology Laboratory, uses fractal geometry to analyze heights of range plants traced by airborne lasers. The heights reveal vegetation type—grass, shrub, or transition zone from grass to shrub. Vegetation type is important to predicting soil moisture, because it affects roughness of land surface. The roughness influences windspeed which in turn greatly affects evaporation of water from soil and water uptake by plants.
G. LeRoy Hahn, former head of the Biological Engineering Research Unit at the U.S. Meat Animal Research Center at Clay Center, Nebraska, and his colleagues Roger Eigenberg and John A. Nienaber used fractal geometry with cattle body temperatures to determine that steers begin to suffer heat stress when the air temperature reaches 77oF. Hahn recently retired but continues his work as a collaborator.
Yud-Ren Chen, who was in charge of the unit at Clay Center before Hahn, also contributed to the animal stress study. Chen found mathematical equations to compute the fractal dimensions of animal temperatures. He now heads the ARS Instrumentation and Sensing Laboratory in Beltsville.
One study was done with six young steers kept in indoor stalls. Sensors in their ear canals automatically recorded their temperatures every 30 seconds for at least 2 weeks, while their stalls ranged from a cool 39oF to 63oF to a hot 80oF to 105oF.
By comparing body temperature fluctuations in the hot and cool chambers, the scientists calculated the fractal dimension. It stayed level at 1.7 until the air temperature reached 77oF. After that, the dimension dropped precipitously to 1.2, indicating that the steers were so heat-stressed they could no longer control their temperatures.
Hahn says that fractal analysis provided a way to assign a number to the degree of fluctuation in body temperature. As the chamber became too warm, the steers became stressed and their temperatures fluctuated less, making the fractal dimension lower. "They were losing their ability to regulate their temperatures. Normally, cows, like people, have marked, random fluctuations in body temperature," Hahn says.
Hahn and Nienaber have since done similar experiments with sheep and pigs.
"Using the fractal dimension of 1.7 as a stress threshold, we can now tell feedlot managers that it's best to turn on their sprinklers when the air temperature approaches 80oF," Hahn says. "We've found this stress threshold correlates well with temperatures at which steers begin to lose interest in feeding."
Hahn also says that observations of individual steers with higher temperature thresholds raise the possibility of using the stress threshold to help breed more heat-tolerant cattle.
Whether data collection is done with livestock or with landscapes, up close or far away, the agricultural research world is finding that fractal geometry may be a way to find order in chaos.—By Don Comis,Agricultural Research Service Information Staff, 6303 Ivy Lane, Greenbelt, Maryland 20770, phone (301) 344-2748.
Yakov Pachepsky is at the USDA-ARS Remote Sensing and Modeling Laboratory, Bldg. 007, 10300 Baltimore Ave., Beltsville, MD 20705-2350; phone (301) 504-7468, fax (301) 504-5823.
Bahman Eghball is in the USDA-ARS Soil and Water Conservation Research Unit, University of Nebraska, 119 Keim Hall, Lincoln, NE 68583-0934; phone (402) 472-0741, fax (402) 472-0516.
Lajpat R. Ahuja is in the USDA-ARS Great Plains Systems Research Unit, P.O. Box E, Fort Collins, CO 80522-0470; phone (970) 490-8315, fax (970) 490-8310, e-mail
Lawrence J. Sikora is at the USDA-ARS Soil Microbial Systems Laboratory, Bldg. 318, 10300 Baltimore Ave., Beltsville, MD 20705-2350; phone (301) 504-9384, fax (301) 504-8370.
Raymond R. Allmaras is in the USDA-ARS Soil and Water Management Research Unit, University of Minnesota, 439 Borlaug Hall, St. Paul, MN 55108; phone (612) 625-1742, fax (612) 649-5175.
Walter J. Rawls and Jerry C. Ritchie are at the USDA-ARS Hydrology Laboratory, Bldg. 007, 10300 Baltimore Ave., Beltsville, MD 20705-2350; phone (301) 504-7490, fax (301) 504-8931.
John A. Nienaber, G. LeRoy Hahn, and Roger A. Eigenberg are at the USDA-ARS U.S. Meat Animal Research Center, P.O. Box 166, Clay Center, NE 68933-0166; phone (402) 762-4270, fax (402) 762-4273.
Yud-Ren Chen is at the USDA-ARS Instrumentation and Sensing Laboratory, Bldg. 303, 10300 Baltimore Ave., Beltsville, MD 20705-2350; phone (301) 504-8450, fax (301) 504-9466.
"Fractals—A Bridge to the Future for Soil Science" was published in the April 1998 issue of Agricultural Research magazine. Click here to see this issue's table of contents.